Math can be really fun. Seriously.
This post is the 2nd in a series of posts I’m planning to have about why math is such a beautiful, useful, and awe-inspiring subject, and that a lot of us can do math (advanced/seemingly difficult math even). Math is such an integral part of humanity since our cave dwelling days, and much more so now in most of our technology driven lives. Previously I wrote about how even advanced math, particularly advanced geometry, can be easily tackled with just your imagination. This time it’s about probability. I can just imagine some of you cringe at the thought of math, let alone probability. But I’ll try to show you that often times, logical reasoning is all that it takes to wrap your head around probabilities, even the ones that confound a lot of brilliant people, even some mathematicians themselves. In fact, we’ll end this article with a simulation of a game/game show. Not bad huh? 🙂
Probability and people
In a nutshell, probability is the area of math which deals with the likelihood of an event happening. It is usually expressed as a number, whether a fraction or a decimal, between 0 and 1, with a probability of 1 meaning the event will surely happen and a probability of 0 meaning the event won’t happen.
Now, don’t be too hard on yourself thinking that probability is too hard for you, unlike most of the human population. In fact, probability is one really confounding area of math and problems in it that seem to be easy in hindsight, turn out to be deceptively difficult or tricky, even for mathematicians, teachers, and other brilliant men and women around the globe. In fact a lot of us have trouble wrapping our heads around probabilities. You mix that with human hopefulness and also the difficulty of grasping very large numbers and what you get is the staggering number of people around the world falling in line to get their lotto tickets so they could win the multi-million prize money.
In fact, if we do the math, in a typical 6/49 game of lotto (6 unique numbers chosen out of 49 numbers, where the order of the 6 numbers is not important) we find that your chances of winning today after buying that lotto ticket is 1 in about 14,000,000. So if Lucy (one of the earliest hominids/proto-humans known to us) or her people, or perhaps even Neanderthals started betting on the lottery at the beginning of their lives, some of them should be millionaires by now. That’s how bad we are at assessing odds, especially coupled with large numbers. So when you go buy that lotto ticket later, I’m afraid the odds are so much against you.
However, I’ll discuss next a particularly perplexing probability problem pondered by people, even brilliant ones, and found the solution to be deceptively trivial after all. Actually, even after you get the explanation, from a practical standpoint it doesn’t seem like so. But the logical reasoning will quite surely buy you out. But don’t fret, all you need again is imagination and logical reasoning. 🙂
Game time
Some of you may have heard/read about the American game show Let’s Make a Deal. The Monty Hall problem (MHP) was named after the show’s host. Simply stated, the rules of the game are as follows:
The game master (GM), has 3 doors: 2 with goats behind them and one with a car behind it. The GM lets you choose one door, which you think holds the prize car behind it. Since the GM’s job is to make you and the audience excited and enjoy the game, the GM opens another door. But since the GM knows the placement of the goats and the car i.e. which door has which item behind it, the GM opens a door which has a goat behind it. Now, the GM poses a question to you: Do you or do you not want to change the door you initially picked i.e. the GM gives you an opportunity to stay with the door you originally picked, or to choose the other door, knowing that one of the doors, which the GM opened, has a goat behind it.
The GM in the show is of course Monty Hall (MH). Now, you’d most probably think that since there are only 2 doors left unopened, that the probability of getting either a goat or a car is now 50/50 or 50% right i.e. it doesn’t matter whether you switch doors or not?
Nope.
In fact, however counterintuitive this may seem, your chances of getting the car at this point of the game doubles if you decide to change the door you initially picked. How? Let’s find out shall we? 🙂
Goat, Car, Goat
Now let’s strap on our imagination and logical reasoning caps to find out how the probability of getting the car increases two-fold if you switch your chosen door, and that it’s not a 50/50 chance of getting the car once a door with a goat has been opened by the GM.
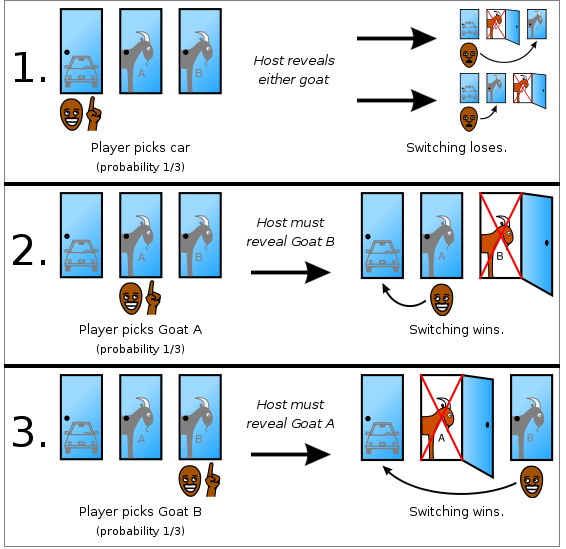
One way of looking at how this counterintuitive probability problem is correctly tackled is by taking the possibility of the events one at a time (refer to the figure above please). In this scenario we show that when you switch doors, you always double your chances of winning. Here’s how:
1. First event, say you picked a door and it happened to have the prize car behind it. Regardless of which door the GM opens, switching in this case either gives you goat A or goat B i.e. you lose the prize car. Out of the 3 possible scenarios (2 of which are listed right after this one), in this one event/case do you lose the prize car.
2. Second event, you choose a door with a goat (goat A) behind it. The GM opens a door again with a goat (goat B) behind it. If you switch in this case, you get the car. This event, wherein you get the car by switching, is one event which you get the prize car. Score one for you. 🙂
3. Third event, you choose the 3rd door with a goat(goat B) behind it. The GM again opens a door with a goat (this time, goat A). So when you switch, you get the car again. Yay. 🙂 This event, wherein you again get the car by switching, is another event which lets you take home the prize.
So what did we get from all this? We saw that out of 3 events/cases of picking either of the 3 doors, you always get 2 events (event 2. and 3.) which favor switching and which lets you walk away with the prize (or in this case, drive away with the prize). So the odds of getting the car/prize in the MHP is not 50% as a lot of us would initially assume, but instead, is really 2/3 or approximately 66.7%.
It can take a while to sink in, but the reasoning/explanation is quite logical and sound.
Try it out!
I actually tried this out with my mother and at another time with my younger brother. What I did was I got 3 opaque plastic cups (simulating the doors) and 2 toy cows (no goat toys in our house at that time) and 1 robot toy that transforms into a car (not bad for a prize no?). I made them act as a GM at one time, with me being the game contestant. Of course to prove my point I always switched. We did this about 20 times and I got the prize car (or robot) at around 14 times out of the 20 (roughly 2/3 of 20). Then I acted as a GM and they acted as the contestant. Then their job was not to switch doors (or cups), just to prove my point that you get the prize more often than not (2/3 of the time remember?) by switching instead of staying with your original door/cup.
They even asked me if I was doing a magic trick on them. I told them it was the power of mathematics and of logical thinking. 🙂 Imagine what much more primitive, let’s say Bronze-aged men, would think of me, with this knowledge, even without modern devices like a cellphone. Perhaps they’d think of me as an oracle or even a god. 🙂
Great, great. But what’s the use?
I think one important thing we can get from this (other than to show you that you can do maths you thought were too hard or complicated for you) is that with math, we can make decisions in our lives (sports betting, lottery, game shows and so on) with more clarity, logic, and sound reasoning, instead of just blind optimism.
If you didn’t get the logic on how to win the game at first glance, or if you thought it was 50/50, don’t be ashamed, a lot of people (some brilliant even) fell for it too. In fact, out of 228 subjects in a study, only 13% chose to switch, and that the rest (87%) assumed that the switching didn’t matter since the likelihood of getting the car out of the 2 unopened doors are equal (research by Mueser and Granberg, 1999).
Quoting cognitive psychologist Massimo Piattelli-Palmarini
“… no other statistical puzzle comes so close to fooling all the people all the time”
and
“that even Nobel physicists systematically give the wrong answer, and that they insist on it, and they are ready to berate in print those who propose the right answer.”
So, not bad eh? Still think math (or at least those areas you think are too advanced or complicated for you) isn’t for the average person? If so, then look forward to my next posts about math. 🙂


@f241vc15: Python running on 32-bit Ubuntu 😉
And I could only wonder how bigger it would have been if it was on a 64-bit system 😛 hehehe
Ah, Python. Yes, Python is quite close to the mathematical, and more I think to the scientific community.
I was thinking of a programming language much older and closer to maths, that's why I thought of LISP. 🙂
durn, people still use LISP nowadays? I remember those antiques from PROGLAN class, hehe. FORTRAN, ADA, SNOBOL… ugh… 🙂
Yes, it's still actually in use, although perhaps more so with the relatively 'older' generation of mathematicians. One lab I know is an IBM innovation lab in the U.S.. Some mathematicians there use still prefer and use LISP to do their research. 🙂
@wes
Yes that would be one (extreme) way of looking at it. 🙂
Ah so Red mentioned this game/puzzle to you earlier/before I even posted this article?
yup, I couldn't get it that time, kasi my mind was wrapped around the thought that the extraneous doors that will just be opened prior to switching were just "pampagulo".
Sometimes exaggerating the numbers help make things more obvious.
Ah I see.
Was my article in anyway helpful at all? Or did it make it worse for you? 🙂
yes it did help. let me see if i get your explanation correctly… its 2/3 because the act of switching makes you lay claim to the opened doors as part of your win-probability?
So if there were 100 doors, switching gives you a 99/100 chance of picking the right door compared 1/100 if you didn't switch?
@wes
Here's another way of looking at the MHP:
Initially, once you pick a door, the probability that it contains the prize is 1/3. The probability however that the prize is in the 2 other unopened doors (we group them together) is 2/3. When the host opens one door in that group, revealing a goat, the probability that that opened door has the prize now becomes 0, and so the remaining unopened door in the group now has the 2/3 probability of it having the prize. So when you switch, you double your chances of winning.
Here's one more way to look at it:
The chances of you getting the prize if you switch, is always 1 minus the probability of getting it correctly the first time you pick a door. So to answer your question about 100 doors, switching does give you a 99/100 probability of getting the prize.
Did I clarify it or did I make it more confusing?
You said: "Now, you’d most probably think that since there are only 2 doors left unopened, that the probability of getting either a goat or a car is now 50/50 or 50% right i.e. it doesn’t matter whether you switch doors or not? Nope."
I think there is a little confusion here. I think the probability of getting either a goat or a car NOW (starting at the point AFTER the contestant chooses a door and when the GM opens a door to show a goat) is 50/50. Remember, probability has no memory. But if we include the first step (contestant chooses a door) in the computation of the probability, switching doors after the GM opens a door does make the probability of winning the car 2/3. 🙂
Finally na-gets ko na sa wakas. I couldn't wrap my head around it when Red first explained the puzzle to me.
Mas madali ma-imagine pag isipin mo there are a gazillion doors and the host opens all but 2 of the doors. If you didn't switch, the chances of picking the right door from the start would be almost impossible but if you switched, you'd pick the right door half of the time.
Oops sorry @wes, you don't get to pick the right door/prize half (50%) of the time. Rather, you get to pick it 2/3 (more than 50%, approximately 66.7%) of the time. That is, when the GM has already opened one door, leaving 2 doors closed.
@cookiemonster: Damn! I AM rusty. LOL. Thanks! 🙂
No problemo 8)
theres another way to think about this… the probability you get it right before any door opening is 1/3. probability of getting it wrong is 2/3.
in other words, considering the 2 unopened, unselected doors as a group, the probability that the prize is is that group is 2/3. i'll call this the "2/3's group"
when the GM opens 1 door in the "2/3" group, the 2/3's groups will only have ONE door in it.
so, to recap, the probability u are right is 1/3, probability u are wrong is 2/3.
since there is only 1 door remaining in the 2/3's group, the probability that you are wrong is still 1/3, you have to switch to the choice that maximizes your chance of winning — the remaining door of the 2/3s group.
oops, mistype, the last paragraph should read, …the probability that you are right is still 1/3, you have to switch to the choice that has the greater chance of winning…
I am really getting rusty at probability. Let me try again:
P = 1/50^6 x 6!
P = 1/15,625,000,000 x 720
P = 1/21,701,389
Now I'm not very familiar with the Lotto if the number 00 is included. If 00 is not included, then there are only 49 numbers. If so:
P = 1/49^6 x 6!
P = 1/13,841,287,201 x 720
P = 1/19,224,010
The formula for combinations is:
n! / (k! * (n-k)!
so in the case of the 6/49 Lotto:
= 49! / (6! * (49 – 6)!)
= 49! / (6! * 43!)
= 608,281,864,034,267,560,872,252,163,321,295,376,887,552,831,379,210,240,000,000,000 / (720 * 60,415,263,063,373,835,637,355,132,068,513,997,507,264,512,000,000,000)
= 13,983,816
NB. I'm not a math wizard, I simply used a simple computer program to get these long, big numbers 😉
@cookiemonster
Math wizard you say, with regards to manipulating large numbers? I think those are indeed extraordinary people, but math does not need to involve the unique ability of manipulating large numbers. You'd be surprised how many mathematicians dislike multiplying several digit long numbers using their heads or even paper.
They instead like thinking in theoretical, abstract or generic ways (e.g. assigning the large number as the variable X), instead of directly manipulating the numbers themselves. Or as you've mentioned, they use computer programs/simulations.
Perhaps you can stay tuned to my future posts about maths to dispel myths about maths. 🙂
Yes, that's quite true, there's less work on really big numbers except, perhaps, for work at scanning electro microscopes and atomic colliders 😉
The programming language I used to derive the big numbers, coincidentally, is also used in some European laboratories. It can handle—and print—numbers as large as 997! (factorial of 997) without using additional libraries. No, that's not a misprint 8)
@cookiemonster
Yes, if they bothered solving those large numbers in their heads or even on paper, they'd finish the whole day with not so much progress at all. 🙂 So the computers do the 'dirty work' i.e. the computations, while they focus on their work/research.
Can I ask what programming language you used? LISP?
@innerminds and @cookiemonster
Yes that's one way of getting the approximately 14,000,000 odds of a 6/49 lottery. The number 0 is not included if I'm not mistaken.
So the odds for getting the first number is 49. The second number is 48, 1 less than the first (since you already picked one number out of the 49). 3rd number has 47 odds.
So in all, you have 49*48*47*46*45*44 = X.
Now, since the order of the 6 numbers is not important, you have to divide X with the total number of combinations you can get from an unordered number of 6 digits (which is 6*5*4*3*2*1 = 720). So X divided by 720 should give you the number cookiemonster arrived at, which is approximately 14,000,000.
Better?
Could you show us how you arrived at the 1/14,000,000 odds of winning the lotto?
I'm a bit rusty on probability, so please tell me if my computations are wrong:
Probability for getting all 6 numbers (ranging from 00 to 49 = 50 numbers) in ANY order:
P = 1/50^6 / 6!
P = 1/15,625,000,000 / 720
P = 1/21,701,389
You are the only person who was able to successfully explain this to me! Thank you.
On switching – most people will not switch because of regret minimization. People will statistically prefer the status quo rather than switching because if they switch, they will feel more regret because of the active decision to switch.
@sinisterpark
I'm glad the article was quite helpful.
That's an interesting point there about switching and regret. Is that one technical term for it, regret minimization? And this is where, economics? Psychology?
Unfortunately this is where the counter intuitiveness of the MHP comes in, that you'll most likely feel regret in case you switch and it turns out you're wrong. But if you knew beforehand and you've logically inferred the probability, then you know you have a better chance when you switch.
Its from her readings for CFA. Finance Related stuff.
As Justin said, I learned it under my readings in Behavioral Finance for my financial analyst certification. It's psych related. Here are some quick links on it:
http://pagesperso-orange.fr/pgreenfinch/bfglo/bfg… http://www.investorhome.com/psych.htm
The concept is applied with regards to behavior of individual investors making an investment decision. Behavioral finance in general makes the proposition that humans are not rational decision makers, and explores that idea and how it affects investment decisions. The concepts seem to apply to other types of decisions as well. It's related to why, for example, if a stock's price goes down, a person still won't sell the stock. They would rather ride the trend and hope for a reversal than sell, only to find out the price recovering a day or a week later. The survey stat you cited also seems to support this theory to some extent (but maybe subconsciously? I'm not sure). Perhaps it is possible that the subjects didn't want to switch not because switching has no perceived positive effect on their chances, but perhaps because the result of switching has great negative potential effect (regret of loss).
@justinaquino/@sinisterpark
Thanks for the added info. That is indeed interesting.
With regards to the statistics/study made on the MHP, it does seem to support regret minimization, since as mentioned already, the MHP is very counter intuitive at face value.
So it makes the assumption that human nature (?) is irrational eh? I suppose if you put it that way, then the threat of great negative potential effect might seem a very likely candidate for many people (87% in the study) not to switch.
maybe its a case of mental inertia? people are content to stay put unless you offer an alternative that is obviously more enticing right off the bat.
or like how most people are content to stay in their current jobs even though there's probably a good chance there's a better job out there if you look hard enough. But since you don't know what the correct odds are, you stay put. Sometimes its the effort of switching that turns people off. you're already expending effort for something that may not even make a net difference.
@wes
those are interesting points.
Early in my college years I wanted to shift to computer science, instead of my original course. But I realized the papers I needed to submit and the lines I had to fall in line in, and so I just stuck myself with computer engineering. 🙂
Wait, I think I was the one confused. LOL. Yeah, I think you're right. 🙂