Mathematics is for everyone. Really.
This article ( and the succeeding ones in the series) aims to prove that point. That everyone has a mathematical brain. Specifically, I’ll concentrate on a certain area of mathematics in this article known as geometry, and then go to more advanced geometry (usually college or graduate level geometry). Don’t fret! There are no equations here which will make your eyes wander and do something else (at least while you’re reading the article). There are a lot of science articles around, but what you usually don’t get often are articles about math, how beautiful and useful it is, and how important it is to science and modern civilization.
A Short Love Story
I love math. That’s how I feel about it: I’m passionate about it, just as I am a passionate about science (particularly physics), sci-fi (Star Trek et al) and technology (programming, software et al). However I started out disliking math in grade school. Like many things in my life which started with me disliking them but ended up with me liking them instead, my love for math grew more and more as I progressed through grade school, then through high school and then college. I disliked math at first because I didn’t pay much attention to studying it, and considered it far less important and impressive than science at that time. The effect then was that I performed poorly in math. As I paid more attention to math however, I learned I was quite skilled at it, and that it was fun for more than one reason. In short, as the years progressed and I learned and matured along with math, I fell in love with it as well.
The Real Mathematical Deal
Unfortunately a lot of people (all over the world you’d be surprised, even in well-developed countries like the UK and the US) both young and old struggle with math. Oftentimes you’ll read/hear news about how kids from different countries around the globe, from grade school and so on, struggle with math. They are usually victims of many unfortunate circumstances which I don’t think , mind you, include not having what is commonly labeled as a “mathematical brain”. Humbug. These circumstances I refer to include a poor/ineffective educational system, poorly trained/ineffective teachers, lack of support from people around you, or combinations of those. Those of us who turned out to love and appreciate math for its beauty, purpose, and elegance, are the fortunate few I think. The exceptions to the rule perhaps. But like I said, humbug. Everyone is born with a mathematical brain, it’s just that we don’t realize it most of the time.
Most of us think about long, boring, frustrating, confusing (and perhaps frightening sometimes?) equations when we think about math. Our grade school teachers made us memorize the multiplication table from 1 to 10 (I heard some even go as far as 15). In high school we learned algebra, or perhaps some of us didn’t, unfortunately. Perhaps some of you later on in life cursed (or still curse) the Arabs for improving and making algebra very widely known and used.
The truth is, mathematics is a large collection of sub-areas of interest, and algebra is but one of them. Some,as you may already know, include geometry, trigonometry, discrete math, and so on. In this post, which is one among a series, I will show you that not only do you have a mathematical brain, but that you can grasp even advanced ideas, in this particular case, geometry. Now let’s get to it shall we? ![]()
Dimension hopping
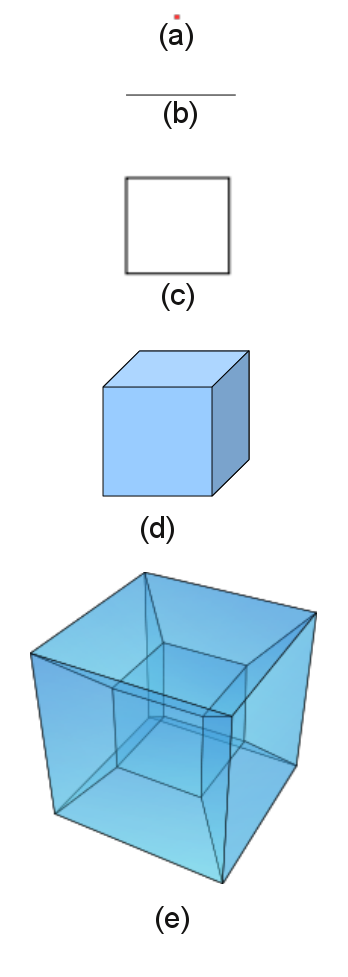
Please observe the figure below (Figure 1), which includes objects (a) to (e). We first start out with an object with no dimension, which is a point in space (a).
Then, if you have two points, connect them together and you have a 1 dimensional object, a line (b). In fact, if you recall your basic high school geometry, a line is just a series of points. The only dimension in this case is of course the dimension of length. So far so good?
Now, if you have a line (b), and then another one similar in length as well as parallel to it, connect their ends and you get a square (c). Now you have a 2 dimensional object, which has both the dimensions of length and width. See where this is going?
Next, if you have two squares which are of the same size, you connect their edges and you get a cube (d). Obviously this is a 3 dimensional object, having width, length, and height/depth.
Finally, and usually this is tackled in more advanced math/geometry courses in college, we extend the 8 corners of the cube and get what is known as a hypercube, in this case a 4 dimensional hypercube (e). You can also imagine this as a smaller cube within a larger cube, and then you connect their edges.
You’d notice that, in order to go to higher dimensions of cubes, you’d just keep on extending and connecting their edges/corners. Easy as pie no? And you just had a 101 on advanced geometry. Many people don’t know that math, especially in advanced courses, involves a lot of imagination and creative as well as abstract thinking. Cool no? ![]()
Great, great. But what’s the use?
What’s the use you say, old chap? What’s the use of knowing how to create hypercubes? Why, quite a lot actually. Aside from the cool realization that you just used your imagination to waltz through an advanced math/geometry class, hypercubes such as the 4D one in the figure (e) have lots of uses.
One is aesthetic. As you can see in the figure below (Figure 2), the Grande Arche in Paris, France is quite a beauty, and one hell of a tourist attraction. It looks so futuristic to me too. It’s inspired by a 4D hypercube such as the one shown above in Figure 1 (e).

Another is that hypercubes are used in supercomputing, or computing that involves trillions upon trillions of data. Supercomputing is necessary and used in weather modeling and prediction, aircraft design, and other scientific and compute-intensive areas and applications. The interconnections of the computers are in 4 or more dimensional hypercubes.
And lots more. In fact, we may still discover more uses for hypercubes in the future. When hypercubes were first realized and imagined many many years ago, mathematicians didn’t really know what good they were for. It was just that it was their work to do math, they were curious, bored, or something in between. What they didn’t realize is that their work would pave for more wonders which our generation now enjoy and is rarely aware of.
So, still think math (or at least more than one area of knowledge in it) isn’t for you? Or that it’s hard to get into advanced math? If you don’t think so, or that you’ve slightly changed your opinion about the topic (about math not being for everyone) then my article has somehow served its purpose. If not, then keep reading my future posts on how everyone can do, use, and even love math as I do. Perhaps even more. ![]()
This article, like many others, was originally posted at http://f241vc15.wordpress.com.


i just want to correct the statement on parallel lines in non-Euclidean space. There are a number of non-Euclidean spaces, in elliptic space for one no parallel lines could exist whereas in hyperbolic space given a point and a line there are at least two parallel lines that can be drawn passing through that point.
Also the prefix hyper as in hypercube or hypersphere refers to n-dimensional objects with n>2 and not exclusive for n=3 only. The 4D drawing in your illustration is called a tesseract. Of course there are also n-cubes and n-spheres.
[…] blogger who want to hide his identity to the pseudonym f241vc15 shares basic math in his article Gather round kids, it’s time for math. Uhm, the kids he was calling had to be very exceptional since he was talking about the basics of […]
Pahabol:
Could you at least give me your name or a pseudonym, so I can put it in the blog carnival. This will promote your article. My blog is currently averaging 650 hits a day, so it will be a great help.
No need to approve this comment.
Cheers,
Guillermo
The pseudonym that I use is this one, f241vc15. I think sir Nemenzo definitely has seen my blog, since if you'll check/search my blog, I posted there one email conversation of ours (with his permission of course) about God and such. 🙂
If you're a little bit more sociable online (unlike me 🙂 ) You might want to join the Facebook and Yahoo! Group of the Filipino Freethinkers UP Diliman chapter. It's headed by, obviously, UP students and even faculty and is already an established org in the university. You could probably send a request email at:
[email protected]
or just pipe your request/s through me.
Facebook group is at:
http://www.facebook.com/home.php?#!/group.php?gid…
Some of these info you may have already found out through this site which I co-manage with other filipino freethinkers users.
Regards,
f241vc15 //,
This is a nice article. It's so nice to find a nice math article written by Filipinos.
@Guillermo
Thanks amigo. 🙂 If you're still interested you might want to check my other maths related posts here: http://f241vc15.wordpress.com/.
Happy reading fellow Filipino. 🙂
Btw, are you by any chance from UP/UP Diliman? 🙂
Yes. I am currently working there. Regarding your other blog very creative. By the way, did you check my blog? Here's the address:
http://math4allages.wordpress.com.
I've been searching for Filipino math blogs on the net so that I can add them in my blogroll, but my search was in vain. I can't believe only a very few of us write about math. Are you a math major or a math professor in IM? Why not write about math. 🙂
By the way, I am going to include this in my blog carnival. I am posting the second edition on Monday. Here's the link of the second first edition:
http://math4allages.wordpress.com/2010/07/12/blog…
Happy blogging!
Thanks re: my other blog. Mostly it's about techie and geek stuff specifically computers. But maths and sciences are definitely part of the geek culture, so there you go. Then I add some bits of poetry and comic books and such. 🙂
I checked your blog. I hope I get more free time so I can read the interesting articles I scanned there. Really nice stuff + presentation. 🙂
Good thing your search somehow yielded a few Filipino math bloggers. It would be quite a bleak thing if there weren't any. 🙂 I'm a masters student at the department of computer science, but my laboratory and field of research is under theoretical computer science, so you can imagine lots and lots of maths there. 🙂 I'm also under the tutelage of sir Henry Adorna, among others, who have their PhDs in math. I also communicate with Dr. Nemenzo from math from time to time. 🙂
Re: including it in your blog carnival, sure. Be my guest. 🙂
Thanks for the link and I hope to get more time for blogging, including maths, soon. 🙂
@innerminds
Coming soon amigo. 🙂
Hey, I'm still waiting for your article on 'singularity'? 🙂
Hey Math-er
Nice to read another math-loving comment. 🙂 Regarding your theory about why the PH is the worst in math in SE Asia, that makes sense to me actually, though of course we've yet no empirical proof or research to back that up. Interesting thought, since math is also mainly concerned with proving things. 🙂
Regarding the intricacy of math in nature and how people tend to ignore or misunderstand it, I think that can also be said in many other things in general, such as in science or the application of scientific thinking in most of the high impact things we do (politics, governance, employment, environmental acts etc.).
Adapting from Carl Sagan's quotes, he asks why hasn't any religion taken it up to themselves and said that science (which includes math) describes our universe in such a beauty and mystery so many orders of magnitude greater than what any religion has ever conjured or invented in their holy books? Understanding the science and math of nature does indeed make it so much more interesting than what any creation myth can ever produce, as those myths and books are bound by the limitations of the human imagination.
Math is such a wonderful phenomenon wouldn't you agree? You can just look at the Grande Arche image above and marvel at its architectural magnificence for one thing. Since you're a teacher, what do you think of my endeavor to prove that everyone has a mathematical brain, which can do basic to advanced math in several areas of math? Stay tuned for future posts regarding this topic/endeavor of mine. 🙂
Dear f241vc15,
I love the fact that you made a math related post. I believe that it is only through math that one can see the power of logic. I currently teach math and I'm still surprised by the number of religious people in my department (this is probably why we still are the worst in math in SE Asia) since the field of math is the practice of proof.
The problem with the appreciation of math is the conspicuousness of it e.g. patterns in nature. It's in front of us yet it's science is so complicated. Too complicated that people don't attempt to understand it. I think this is where the problem in our society lies. People see a beautiful sunset and people say "Ang galing ni God no?" I say "I'm amazed at how the different light waves go together". Believing in God just takes away the real beauty of nature and I appreciate you for making posts that show us how beautiful it really is 🙂
@f241vc15: That stuff about two 2-dimensional planes intersecting in a single point in 4-dimensional space is indeed hearsay. It was posted in a forum as a question to a new member, a Dutchman. Unfortunately, it was never properly answered although the Dutchman's reply was quite interesting:
"Unfortunately I am unable to answer your question. The native Dutch are very primitive in terms of numbers. The reason for this, as you clearly demonstrated in your calculation, is that a third dimension is perceived when two 2-dimensional planes intersect, and this has never occurred in the Netherlands since (as everyone knows) it is entirely flat, hence we had no need to devise a numeral system for numbers above 2. It was only in Colonial times when rumours of distant lands with mountans, which we only knew from 2-dimensional pictures, reached our ports that the native Dutch could believe there might be a third dimension. After a long time of discussions between religious leaders and a few persecutions of early notable 3-dimensionalists (a part of our history we have successfully managed to hide from foreigners) an enlightened priest pointed out that, even though there was no definitive textual evidence of a third dimension, the Bible as a book supported this idea and thus the Netherlands officially accepted the existence of a third dimension. Successively a number was adopted to describe this particular dimension, which is why we now can count to three.
You may probably have realized from our history we are backwards when it comes to mathematics and we still have trouble adjusting to a 3-dimensional world. This is clearly illustrated in the tendency in nearly every Dutchman to describe everything bigger than themselves as a mountain. I personally believe in a third dimension and I am willing to explore beyond the realms of our common knowledge, but the education I have received is hardly appropriate to understand this concept, let alone further dimensions. I do not mean to hide behind my education. History has proven to us there may be more dimensions than we think and I hope to explore this subject further someday if I can become a foreign exchange student. Just wondering where that would take me, though…"
@Jeiel
That is very intriguing. I should look into that sometime soon. Thanks for sharing. 🙂
I was just listening to the latest radiolab episode which is on numbers. It contained some very interesting information on how our brains develop the concept of numbers. It seems that the natural way that our brains evolved to think about numbers is very different from how adults actually think about numbers. Babies think about numbers in a logarithmic way while adults tend to think about numbers in terms of integers.
Integers is something that civilisation bootstraps onto the brain through education, through parents counting with babies or education. Without integers being taught to us we wouldn't be able to avail ourselves of the useful mathematical concepts that the use of integers.
@Sathepine
Good for you then. I would think that we're the lucky few who don't scorn math, and there are even fewer of us who love and admire math for its beauty and elegance. Memorizing formulas is an unfortunate stage in the study of math. Perhaps our educators or educational systems can address that in the future. But for now, if you go further beyond basic college calculus, past those integral and differential forms of equations, you'd be surprised how little memorization is required in advanced mathematics. 🙂
@innerminds
Sounds to me like the post is more of a religious apologist's statement. 🙂
Here are some hints to my succeeding everyone-has-a-math-brain posts: probability, what really is the curvature/geometry/shape of our universe?, wonders of prime numbers, and so on… 😉
I'm *kind-of* good in math… I liked Calculus back in college (and took an elective of it in high school) but kinda slacked off later on because I prioritized my other more important subjects than memorizing formulas. Never failed though. (That's three subjects of advanced Calculus that I managed to pass, yay!) Okay, I'm babbling ^_^; Looking forward to your future posts…
@innerminds/Sathepine et al
About not being good in math, let's see if my succeeding posts will convince you otherwise i.e. you can do advanced math which you didn't know existed or that you could do them. 🙂
@innerminds
One possible explanation is perhaps the planes in the quotation aren't infinite at all, hence they really can intersect at a single point, and not necessarily in 4D space.
If however the planes referred to are indeed infinite, I'm not exactly sure how intersection at a single point can be achieved. Based on your quote though it sounds more like hearsay to me. 🙂
Nevertheless, it depends on many other details/factors, such as what geometry you also use. In fact, in non-Euclidean geometry (Euclidean is what most of us study) parallel lines can intersect! How weird is that? 😀
Another would be that the planes, although finite, are boundless, such as a sphere. As for being flat, "flat" is a relative term, as you may realize, since the Earth is quite spherical but appears to be flat in our POV. In the case of spheres, planes can really intersect at one point only, which is the point tangent to both spheres.
@innerminds/@Sathepine
I hope I've answered your questions adequately. If not, let's try more abstract thinking and imagining next time. Math rules. 😉
For more math fun (albeit a bit more technical, just a tad bit more 🙂 ) checkout an older post of mine: http://f241vc15.wordpress.com/2008/02/17/reflecti…
@f241vc15: I'm not very good in math, but I stumbled on the following while surfing the net:
"We all know that in 3-dimensional space, two 2-dimensional planes can intersect in a line. But I heard that in 4-dimensional space, two 2-dimensional planes can intersect in a *single* point.
Can that really happen? It sounds crazy… how can the intersection of two (typical, flat) planes, both infinite in extent, be *exactly* one point, no more, no less?"
Care to share your thoughts? 🙂
@Sathepine
Naive? Not at all. I think that's a fairly reasonable question, and one which I was expecting somebody to ask actually. 🙂
Time being the fourth dimension refers to space-time, as I think you got confused with my my earlier post about the physics of attraction no? The 4 dimensions in this case are forward-backward, up-down, left-right, and time.
In this case, geometry, the 4th dimension could be anything you could imagine. The 3 dimensions in this case are length, width, and depth/height. The 4th dimension could be called jygms for all we care or know. And for now I think, if it has not been named or hasn't found any use, it's just for the curious and the mathematicians. The important thing is we can put hypercubes to good use. 🙂
We use math everyday, in our daily life, in social inter-action even in personal affair.
Many of us has the impression that math is all about numbers instead of logical reasoning.
4D seems a lot like 3D to me. (I thought the fourth dimension was time.. meaning, the object now moves. forgive me if that's naive.)
@joma
Yes unfortunately, the more beautiful, artistic, and poetic side of math is usually never revealed to many people. To most I think, math is just about manipulating numbers upon numbers.