The Most Powerful Force in the Universe (Part 1)

A Tale of the Two CEOs

One day, two bold CEOs decided to play a game of chess where the winner gets to ask anything he wants from the loser. After the game, the winning CEO asked the losing CEO to choose between two payments. The first payment involves the losing CEO giving half of his company’s assets to the winning CEO. The second payment involves placing 1¢ in the first square of the chessboard, 2¢ in the second square, 4¢ in the third, 8¢ in the fourth and so on until all the 64 squares of the chessboard are filled. Thinking that it will allow him to get off easy, the losing CEO agreed to the pay the winning CEO the second reward. But the losing CEO made a very serious mistake. In the process of trying to pay the winning CEO the reward, the losing CEO ended up going bankrupt and buried in debt. In fact, the losing CEO may never be able to give the reward money even if he spends his whole life working for it.^[1]

Double, Double, Double….Jeopardy!

Human intuition evolved to understand linear progressions and patterns only. For many everyday purposes, this intuition is a quick and effective tool in assessing odds and projecting future values. The losing CEO’s big mistake is that he used the said intuition on an example where it is not applicable, an example that involved not a linear progression but a geometrical one.^[2]

When you add up the terms of an increasing geometric progression, what you get is exponential growth.^[3] As with geometric progressions, the human brain is notoriously ill equipped in understanding the power of exponential growth. This is shown by the fact that, without the aid of mathematics, almost all of us find it difficult to understand why the losing CEO made such a grave error. In order to comprehend the gravity of the losing CEO’s mistake in choosing the second payment option, let us get rid of our intuition for the moment and let us turn to mathematics.

Imagine starting with x of something. If you double that number, it becomes twice the original, 2x. If you double the previous result, you get four times the original, 4x. If you keep on doubling the most recent result, you’d successively get 8x, 16x, 32x, 64x and so on. Notice that doubling once gives you 2x or 2¹x while doubling twice gives you 4x or 2²x. Meanwhile, doubling thrice gives you 8x or 2³x and doubling four times gives you 16x or 2⁴x. Following this pattern, we can see that doubling x an n number of times gives you 2ⁿx.

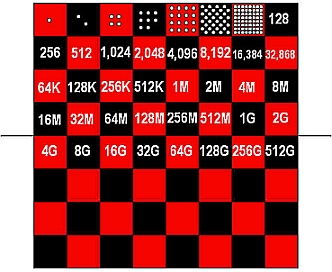
Recall that the losing CEO started with a mere 1¢ (that is, x = 1¢). By the 8^th  square (the last square in the first row) he is required to double the original 1¢ seven times. This means that he must place 2⁷ times 1¢ on the 8^th square. Using a simple calculator, one can easily confirm that 2⁷ = 128. This means that the 8^th square must contain 128¢ or $1.28. So far, the losing CEO still feels he’s having it easy. However, when he reaches halfway through the chessboard (the 32^nd square), he would have doubled the original value 31 times. This means that the 32^nd square must contain 2³¹ times 1¢. Using a calculator, one can compute that this amounts to 2 147 483 648¢ or around 21.5 million dollars! But the tragedy of the losing CEO is only beginning; even though at this point he is halfway through the chessboard, the losing CEO is still very far from paying half his due. By the time he reaches the last chess square, he is going to need a whopping 92 million billion dollars! But wait, there’s more. The said 92 million billion dollars is for the last square only. Adding up the amount of money he must place on all 64 squares of the chessboard, the total amount of money the losing CEO owes the winner is approximately 184 million billion dollars!^[4]

The Curious Case of Exponential Growth

Here’s another example of how wildly counter-intuitive exponential growth is. Imagine starting with a piece of paper (of thickness 1.0 mm). Fold that paper into two halves so that its new thickness is twice the original. Now fold it again so that its thickness is four times the original. If you repeat this process just 42 times,^[5] you end up with a piece of paper that will extend from the surface of the earth of the surface of the moon!

A very peculiar aspect of exponential growth that the human brain finds so hard to understand is the fact that if something grows exponentially then the present value is greater than all the previous values combined. For example, notice that the amount of money the losing CEO must place on the 5^th square, for example, is greater than the total amount of money he must place on the 1^st, 2^nd, 3^rd and 4^th squares. This is true even for the 64^th square – the amount of money it must contain is greater than the sum of the contents of the remaining 63 squares.

Exponential Crises

Albert Einstein once said, “The most powerful force in the universe is compound interest.” Since the mechanism behind compound interest is exponential growth, the previous example shows that Einstein’s humorous hyperbole is only partly so.

Big companies, especially banks, tap into the power of exponential growth to get rich. But big companies pay decent sums to their actuaries and analysts to deal with the number shuffling involved in compound interests (in the interest of compounding their profit and compounding your debt). In the absence of such expertise, unaided human intuition will more often than not fail in assessing problems involving exponential growth.

An individual’s failure to appreciate the power of exponential growth usually leads to debt crises.  The losing CEO is just one (rather fantastic) example of the victims of the human brain’s inability to grasp exponential growth. To give a more common example, the many people who are buried in credit card debts are similarly victims of the failure of human intuition to grasp the full force of compound interest and the mechanism behind it, exponential growth.

In many ways, the losing CEO represents human civilization. Many of the problems we face today as a society stems from our failure to assess the power of exponentially growing quantities around us. Like the losing CEO, we use our linear human intuition to analyze situations involving geometric progressions and we end up engulfed by the problems this wrong judgment caused.

Three of the greatest problems caused by our failure to grasp exponential growth are:

• the human population explosion
• the rapid (or should I say rabid) increase in human demand for resources leading to the even more rapid depletion of natural capital
• the rapid increase in industrial activity leading to uncontrolled increase in the generation of pollution and waste

I will write about the other two global problems in future articles. In Part 2 of this article, however, I will concentrate on the first and perhaps most important the three – human population explosion. I say it is the most important because it is the key to solving the other two problems; the problems of resource depletion and environmental degradation cannot be fully addressed without addressing population explosion. Finally, it is the human population explosion that I will write about in Part 2 because it is an urgent national issue that is intimately related to the debates regarding the passage of the RH Bill.

Click here to read Part 2.

 * * *

Notes:

^[1] Adapted from a version of the legend of Paal Paysam told on Reference [1].

^[2] An arithmetic progression is a sequence of numbers in which the next number in the sequence is just the previous number plus a constant. Examples are the sequence {1, 2, 3, 4, 5, …} and the sequence {4, 7, 10, 13, 16, …}. In the first progression, the constant being added is 1 while in the second it is 3. A geometric progression, on the other hand, is a sequence of numbers in which the next number in the sequence is just the previous number times a constant. Examples would be {5, 15, 45, 135, 405, …} and {2, 4, 8, 16, 32, 64, …}. In the first sequence, the constant being multiplied is 5 while in the second it is 2. Notice that the second progression is simply the progression our losing CEO is having a problem with. Geometric progressions, however, can also be decreasing, just like the sequence {4, 2, 1, ½, ¼, …}.

^[3] The sum of the terms of an increasing geometric progression increases exponentially as you increase the number of terms being summed up. For those who know their math jargon, this can be expressed by saying that the partial sum of a monotonically increasing geometric series diverges. The result for a decreasing geometric progression is similarly tricky to the human intuition and is at the root of Zeno’s Paradox. The apparent Paradox is resolved if one understands that a sum of infinitely many numbers can be finite if the numbers being summed up form a decreasing geometric progression. That is why 4 + 2 + 1 + ½ + ¼ + … = 8, even though you are adding infinitely many numbers.

^[4] For those who recall their college calculus, the formula for the nth partial sum of a geometrical series with 1 as its first term and 2 as the common ratio is given by the formula s_n = (rⁿ – 1)/(r – 1). Here, r = 2 and n = 64. The total amount of money the losing CEO must place in all the 64 squares of the chessboard is just equal to the partial sum s_n.

^[5] Douglas Adams is God.

 ^{* * *}

References:

[1] Miller, G. Environmental Science, 10th ed, 2005.

[2] Arfken, G. B. and Weber, H. J., Mathematical Methods for Physicists, 5th ed, 2001.