Quantum Queries: Where’s Amber?

This is a continuation of the story of Amber the electron. Amber’s story is a very important one because it is also the story of physics, the study of the fundamental aspects of our universe. You may learn about the first part of this story by reading ‘Quantum Queries: Is Ours A Clockwork Universe?’

Down In Amber’s World

Last time, we saw that up here in the world of familiar objects — bouncing basketballs, falling apples, orbiting planets — the laws that govern our universe make it tick like clockwork. Down in the world of Amber the electron, things can seem very different. We must use a different set of rules to explain the behavior of Amber the electron and similarly small objects like protons, neutrinos, and positrons. These are the rules of quantum mechanics, and objects governed by these rules can be called “quantum objects”. Amber the electron is a quantum object.

Back to the questions that started this discussion: Where’s Amber? And how fast is she going? Where is she headed? There are two things we must know about Amber before we can reasonably answer these questions.

First, everything we can say about Amber is contained in what is known as her wave function. The wave function is represented by the Greek letter Ψ (psi). Basically, Ψ contains everything that we can say of Amber.

Second, Ψ can be determined using Schrödinger’s equation (named after the colorful German physicist Erwin Schrödinger).

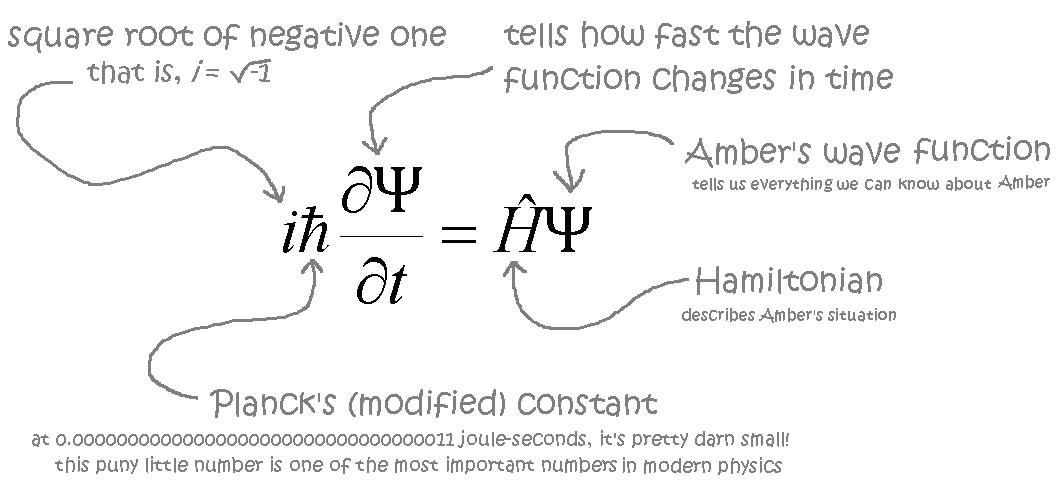
Schrödinger’s equation plays the same role in quantum mechanics as Newton’s Second Law does in classical mechanics. Recall that if we know the location and velocity of Bouncy the ball now, we can use Newton’s Second Law to determine his location and velocity at any other time. Likewise, if we know Amber’s wave function Ψ at any given moment, then we can use Schrödinger’s equation to determine Ψ at any later or earlier time. In other words, the way the wave function changes over time is also deterministic.

But wait, where is Amber? And how fast is she going? Where is she headed? Where will we find her at some later time?

To answer these questions, we now turn to the crux of the matter and possibly the source of all the weirdness of quantum mechanics. We turn to the meaning of the wave function, Ψ. What is Ψ anyway and what does it tell us about Amber’s whereabouts and howabouts?

Well, scientists have discovered that Amber’s wave function determines her probability density. Amber’s probability density gives us the likelihood of finding her in some place. To illustrate what this all means, let us use the well-known example of the hydrogen atom.

Suppose Amber is the electron of an atom of hydrogen. We can use Schrödinger’s equation to determine Amber’s wave function Ψ. Once we have determined Ψ, we can then use it to determine Amber’s probability density. In the context of atoms, the probability density of the electron is also called its electron cloud. Why is it called an electron cloud? Well, just take a look at the picture below.

The picture shows one of Amber’s possible probability densities, one of her potential electron clouds. (For those who remember their high school chemistry, the electron cloud shown above is what chemists call the ‘1s orbital’.) The darker regions represent regions in space where one is relatively likely to find Amber. Meanwhile, the lighter regions are the regions where finding her is relatively improbable. Notice how Amber’s probability density is diffused throughout space. That is why it’s called an electron cloud– like a cloud, it is not a firm, rigid structure but is instead spread out. Below are more possible electron clouds for Amber. (Chemists call them the 2p, 3p and 3d orbitals, respectively.)

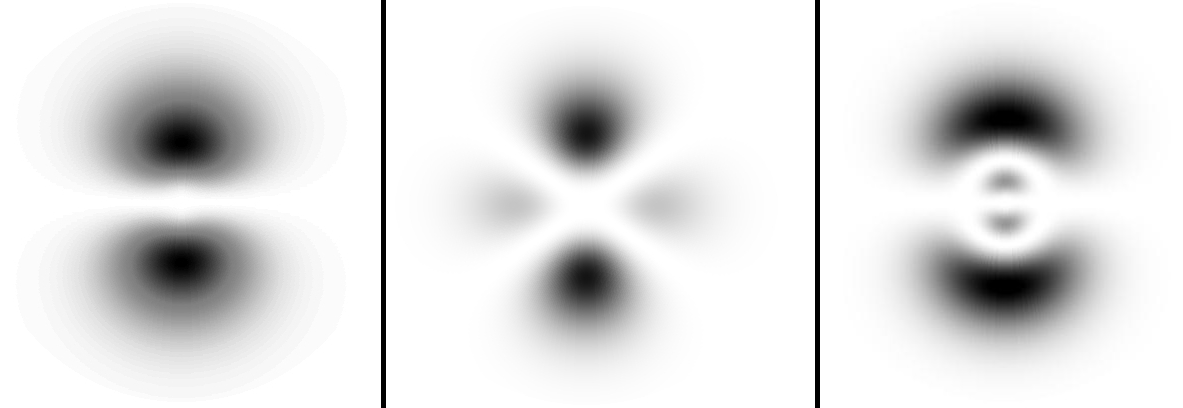
So, does this mean that Amber is spread out? Well, let us check via experiment. Let us consider again the original electron cloud above. This time, we label some of the points in space. Let’s label them points A, B, C and D. Even before we perform the experiment to determine the whereabouts of Amber, we already know that Amber is more likely to be found in A than in B and less likely to be found in C than in D. Also, Amber is equally likely to be found in A as in D.

However, scientist found that after performing the experiment, they find Amber in a definite location. Say, you perform an experiment and find that Amber is in B. Two questions naturally arise. First, why in B and not A, where she was more likely to be found? Second, does the result imply that Amber was in B all along?

To answer the first question, we note that quantum mechanics is different from classical mechanics in being probabilistic instead of deterministic. In other words, quantum mechanics is about probabilities or likelihood. And in probabilities, an improbable event is still possible and can therefore happen, while a probable event does not have to occur. For example, when you throw a pair of dice, getting a 7 is a likely outcome while getting snake eyes is unlikely. However, when you throw a pair of dice, it is still possible, although unlikely, to get snake eyes instead of a 7. The probabilistic nature of quantum mechanics is what inspired Einstein to compare it to God playing dice with the universe.

Now it’s time to tackle the second and thornier question: If we perform an experiment to locate Amber and, as a result, find her in B, doesn’t that mean she was in B all along? There are three main answers to this question, and they represent the three main interpretations of quantum mechanics. They can be stated as follows:

1. The realist position says that Amber was in B all along. However, quantum mechanics was not able to tell us this. After all, quantum mechanics says that everything that can be said of Amber is already in Ψ. However, Ψ did not really tell us where we will find Amber, it merely gave us probabilities. Quantum mechanics is therefore incomplete – it does not give us a complete picture of reality. People subscribing to the realist position believe we need to discover what are known as hidden variables. Once these hidden variables are discovered, we can determine that Amber was indeed in B all this time.

2. The Copenhagen interpretation says that before the experiment, Amber was not in B, nor was she in A, C, D or in some other location. This interpretation tells us that her wave function gives us all we can know about her. This has a very interesting implication: if Amber was not in any place before the search, and was found to be somewhere after the search, that means that the act of looking for her somehow forced her to be somewhere! In the case of our example, that somewhere simply happened to be B, but it could have been A, C, D or some other location.

3. The agnostic position is to be silent about the whole matter. After all, who are we to say where Amber was before we actually searched for her? And it doesn’t matter whether you take the realist or Copenhagen interpretations because the equations of quantum mechanics give you the correct probabilities anyway.

After decades of furious research, many working physicists find themselves subscribing to the Copenhagen interpretation. (The Copenhagen interpretation got its name from the city of Niels Bohr, one of its main proponents.) And, surprisingly, the agnostic position is already eliminated by a relatively recently discovered theorem known as Bell’s theorem. Bell’s theorem basically says that it does make an observable difference whether Amber was in B all along or whether she was nowhere.  Also, very few working scientists are still hoping to find the hidden variables required by the realist position.

There are, in fact, other interpretations of quantum mechanics currently being considered by scientists. One of the more interesting of them is the many worlds interpretation.

4. The many worlds interpretation (MWI) says that all possible outcomes (finding Amber in A, B, C, D and all other possible locations) actually happen, but in different worlds! According to the MWI, what is objectively true is the Universe (with a capital U); it is where you find Amber’s electron cloud. When you try to look for Amber, the many worlds of the Universe decohere; that is, they get distinguished from each other. In one of those worlds, you find Amber in B, and in that world, she was in B all along. In another of those worlds, you find her in A, and in that world, she was in A even before you searched for her. And so it goes for the other possible outcomes (finding Amber in C, D, ect.).

If you are starting to find Amber’s world weird, know that this is only the tip of the iceberg. The world of Amber and her fellow quantum particles is governed by randomness. It is the opposite of the clockwork universe of classical physics.

Quantum vs. Classical

Now, one might think it strange that there are different rules governing the universe at different scales, classical mechanics for big things and quantum mechanics for very small things. How does one decide how big is big, anyway? Or how small should a thing be for it to be ruled by quantum mechanics? The truth is, according to the best scientific evidence we currently have, quantum mechanics governs the behavior of everything. Even Bouncy the basketball is governed by quantum mechanics! After all, Bouncy is also made of electrons, protons and neutrons, which are all quantum objects. Everything around us is made of quantum objects! However, for objects the size of Bouncy, classical mechanics is a good enough approximation. In fact, it is a superb approximation, to the point that we could use classical mechanics to predict Bouncy’s behavior without fear of being wrong. In other words, classical mechanics is an excellent estimate of quantum mechanics that is appropriate in the world of everyday objects. In the scale of things we see and touch, the weirdness that quantum mechanics displays on the small scale disappears.

Given these statements, this article is therefore about the fundamental rules that govern the behavior of everything around and within us. Ours is a quantum universe, and God does indeed throw dice on us all.

Up Next on Quantum Queries:

• What is the deal with Schrödinger’s cat?
• What is Heisenberg’s uncertainty principle all about?
• What is a ‘quantum’ of anything?
• Why did Einstein find quantum mechanics so repulsive?
• What is tunneling and how will it render Moore’s law obsolete?
• What is entanglement and how is it related to teleportation?
• Can we test the truth of the many worlds interpretation?